Top 8 công thức tính diện tích tam giác mới nhất 2025, có ví dụ chi tiết

Bùi Hà My - 11:46 03/12/2024

Góc kỹ thuật

Các công thức tính diện tích tam giác là một trong những công thức toán học mà bạn sẽ được học và áp dụng rất nhiều trong các bài tập của môn Toán học. Và để tính được diện tích tam giác, có rất nhiều công thức khác nhau có thể áp dụng. Nắm được công thức tính diện tích tam giác và áp dụng thành thạo vừa phục vụ công việc học tập lại vừa giúp bạn áp dụng vào các trường hợp trong cuộc sống.

Nếu bạn đang gặp khó khăn trong việc tính diện tích tam giác một cách nhanh chóng, hãy tham khảo bài viết Top 8 công thức tính diện tích tam giác dưới đây của chúng tôi nhé!

Mục lục

Top 8 công thức tính diện tích tam giác mới nhất
Tổng kết

Top 8 công thức tính diện tích tam giác mới nhất

Để tính diện tích tam giác, dựa vào đặc điểm phân loại của tam giác đó có thể áp dụng được nhiều công thức tính khác nhau. Dưới đây là tổng hợp 8 công thức tính diện tích hình tam giác chi tiết:

Công thức tính diện tích tam giác thường

Tam giác thường là hình tam giác có 3 cạnh và 3 góc không đều nhau. Để tính được diện tích tam giác thường, ta phải kẻ thêm một đường thẳng từ đỉnh vuông góc xuống cạnh đối diện.

Công thức tính diện tích hình tam giác thường như sau: S= 1/2 × a × h

Trong đó:

S: diện tích hình tam giác
h: chiều cao hạ từ đỉnh xuống cạnh đối diện
a: độ dài cạnh tương ứng với chiều cao

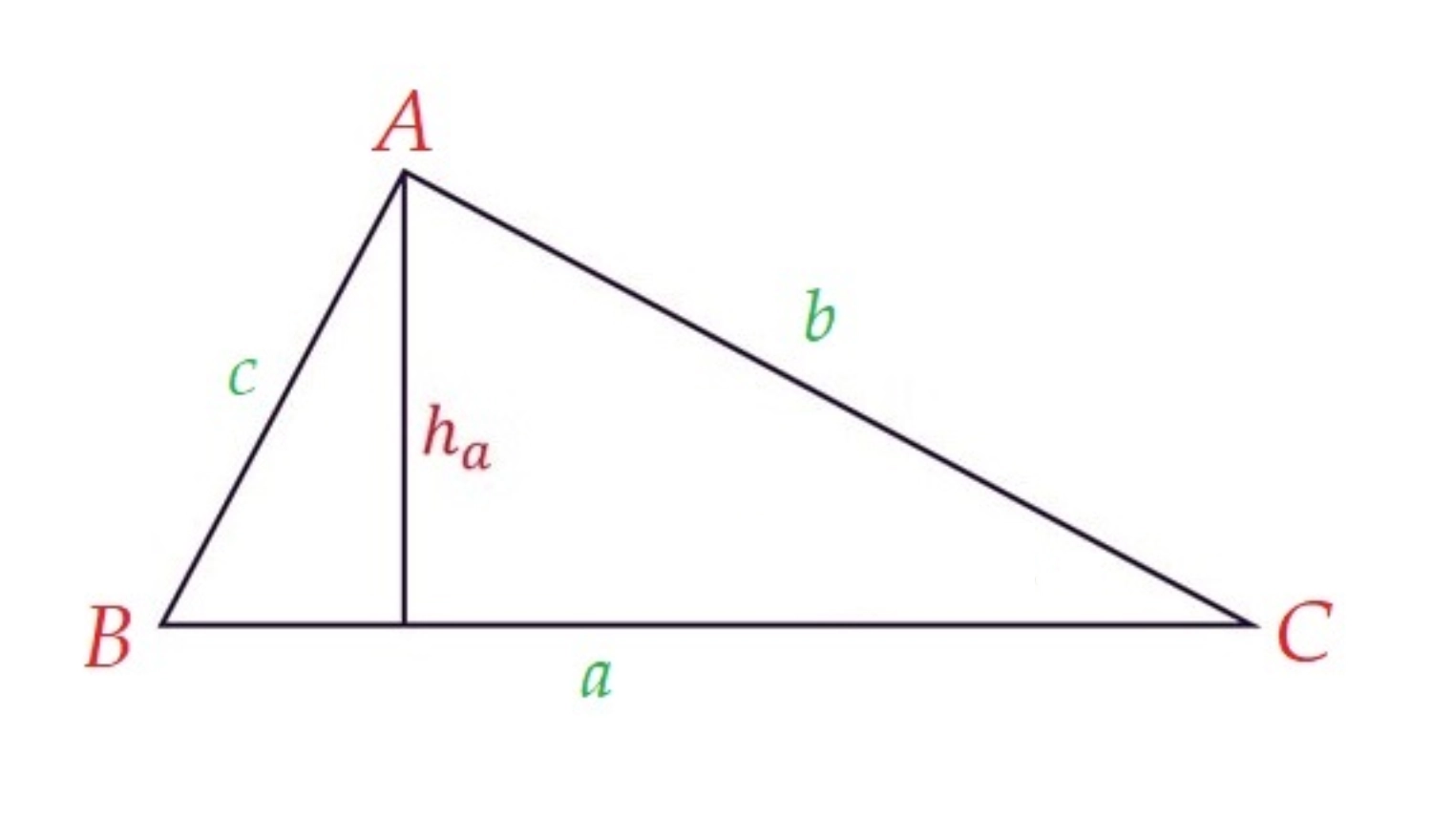
*Công thức tính diện tích tam giác thường*

Ví dụ: Tam giác ABC có độ dài cạnh a là 10 cm, chiều cao h hạ từ đỉnh xuống cạnh A có độ dài là 6 cm. Diện tích của tam giác ABC là: 1/2 x (10 x 6) = 30 cm².

Công thức tính diện tích tam giác vuông

Tam giác vuông là hình tam giác có một góc 90 độ và 2 cạnh vuông góc với nhau. Công thức tính diện tích tam giác vuông như sau: S = 1/2 × a × b

Trong đó:

S: diện tích tam giác vuông
a: độ dài cạnh góc vuông thứ nhất
b: độ dài cạnh góc vuông thứ hai

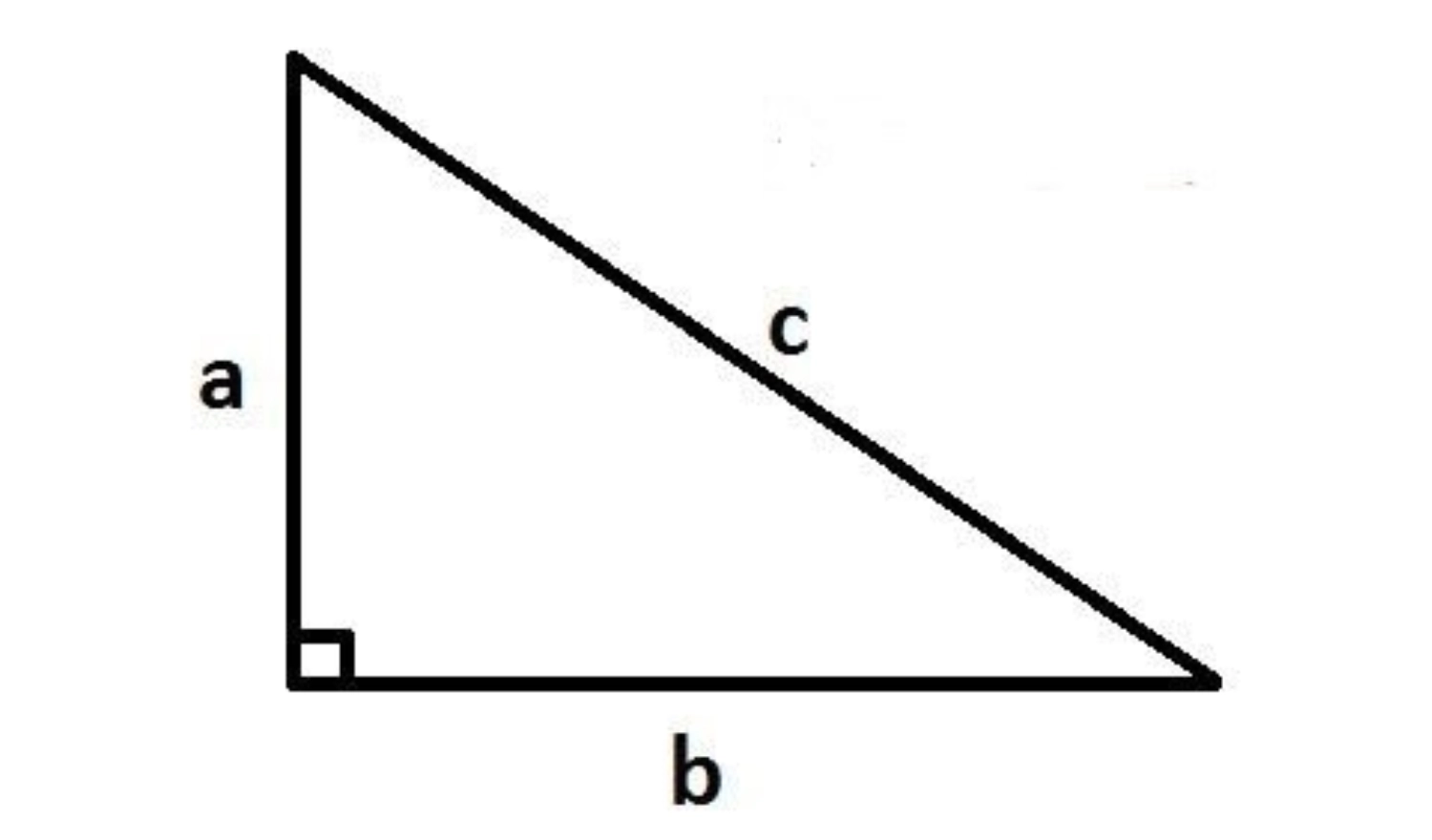
*Công thức tính diện tích tam giác vuông*

Ví dụ: Tam giác vuông ABC có độ dài 2 cạnh góc vuông lần lượt là 6 cm và 10 cm. Diện tích tam giác vuông ABC là: 1/2 x (6 x 10) = 30 cm².

Công thức tính diện tích tam giác cân

Tam giác cân là hình tam giác có 2 cạnh bằng nhau và 2 góc chứa cạnh còn lại cũng bằng nhau. Công thức tính diện tích tam giác cân như sau: S = 1/2 × a × h

Trong đó:

S: diện tích tam giác cân
a: độ dài cạnh còn lại khác hai cạnh có độ dài bằng nhau
h: chiều cao nối từ đỉnh xuống cạnh đáy

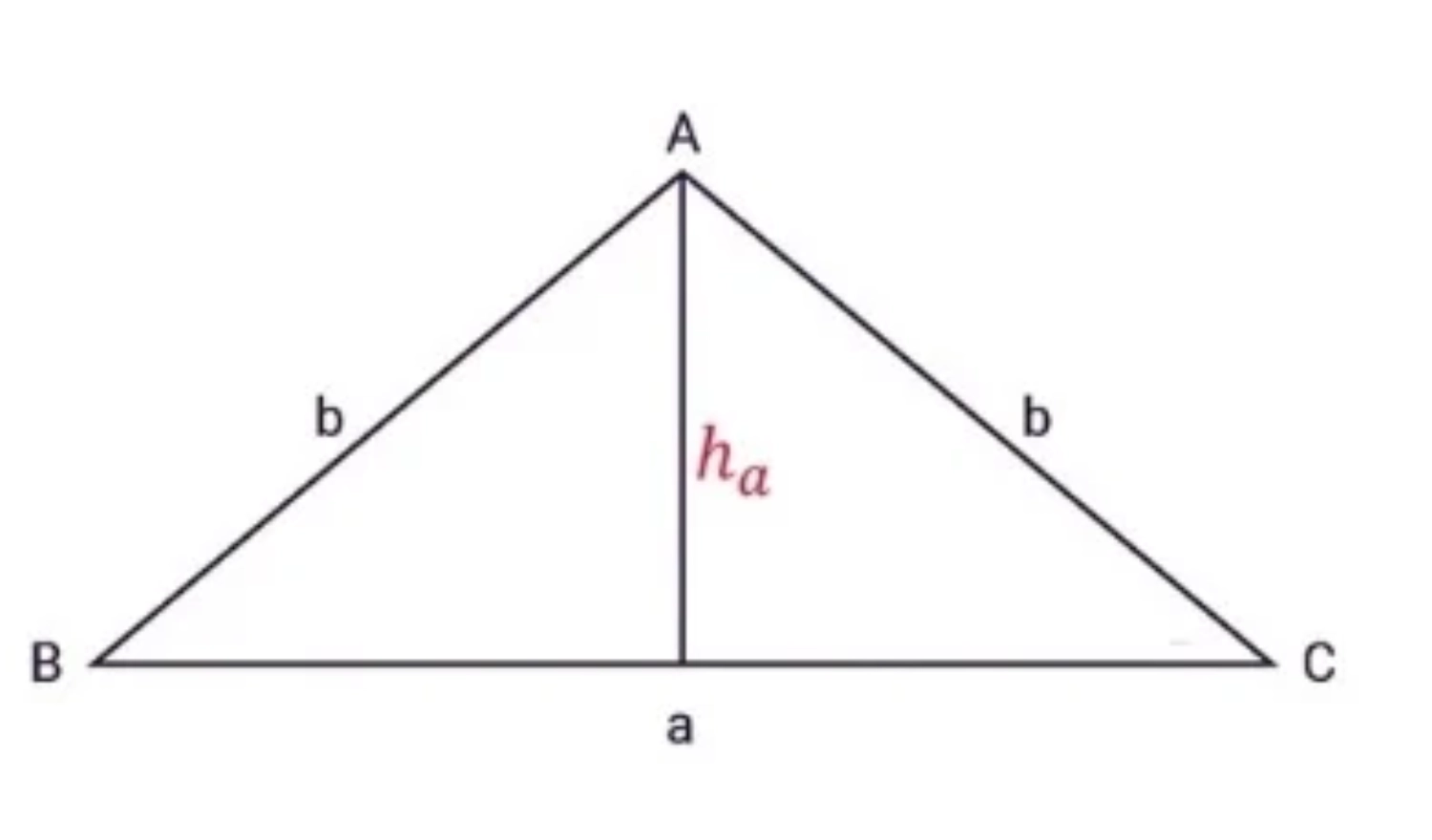
Ví dụ: Cho tam giác cân ABC có độ dài 2 cạn bên bằng nhau, cạnh đáy có độ dài là 10 cm. Chiều cao nối từ đỉnh xuống cạnh đáy có độ dài là 5 cm. Diện tích tam giác cân ABC là: 1/2 x (10 x 5) = 25 cm².

Công thức tính diện tích tam giác đều

Tam giác đều là là tam giác có ba cạnh bằng nhau và ba góc bằng nhau, đồng thời tất cả các góc đều là 60 độ. Ta vẫn có thể áp dụng công thức tính diện tích tam giác như bình thường là: S= 1/2 x a x h.

Trong đó:

S: diện tích hình tam giác
a: độ dài chiều cao kẻ từ đỉnh xuống cạnh đối diện
h: độ dài một cạnh bất kỳ

Ngoài ra do tính chất đặc biệt của tam giác đều, chúng ta có thể rút gọn công thức này thành một dạng khác, tiện lợi hơn trong tính toán, đó là công thức: S = a² × √3/4

Trong đó:

S: diện tích tam giác đều
a: độ dài một cạnh bất kỳ của hình tam giác

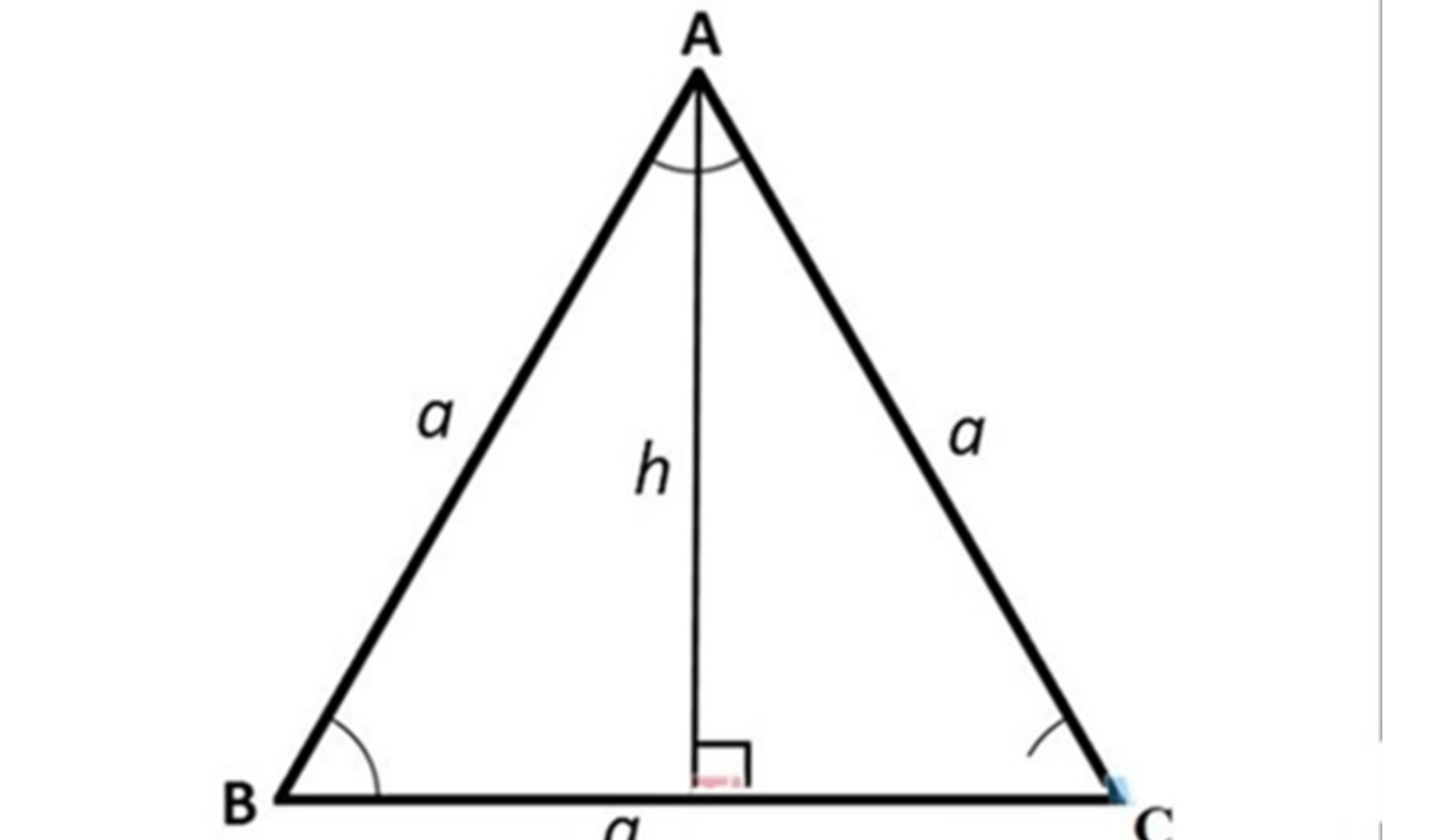
Ví dụ: Tam giác đều ABC có các cạnh bằng nhau và bằng 6cm. Diện tích tam giác đều ABC được tính như sau: 6² x √3/4 = 15,5 cm²

Công thức tính diện tích tam giác vuông cân

Tam giác vuông cân là tam giác có một góc vuông và hai cạnh góc vuông bằng nhau. Công thức tính diện tích tam giác vuông cân như sau: S = 1/2 × a²

Trong đó:

S: diện tích tam giác vuông cân
a: độ dài cạnh góc vuông

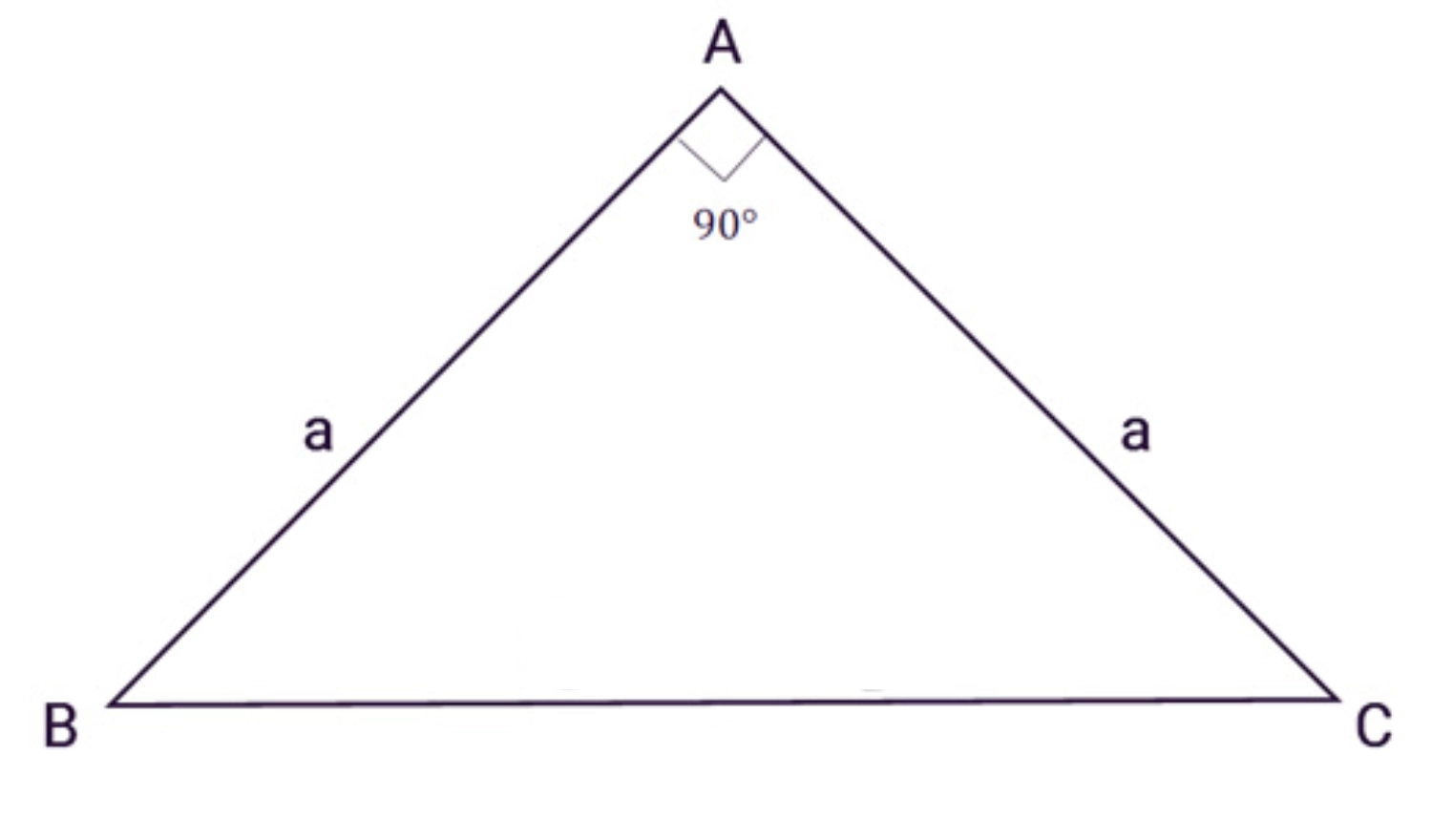
*Công thức tính diện tích tam giác vuông cân*

Ví dụ: Tam giác vuông cân ABC có độ dài hai cạnh góc vuông là 10 cm. Diện tích tam giác ABC là: S = 1/2 x (10²) = 50 cm²

Công thức tính diện tích tam giác theo hệ tọa độ

Ta đều có thể dử dụng các công thức trên để tính diện tích tam giác trong mặt phẳng hay trong không gian với hệ tọa độ Oxyz. Tuy nhiên, như vậy sẽ gặp một số khó khăn trong tính toán và để thuận tiện hơn, hãy sử dụng công thức tính diện tích tam giác theo tích có hướng.

Trong không gian Oxyz, cho tam giác ABC. Diện tích tam giác ABC được tính theo công thức:

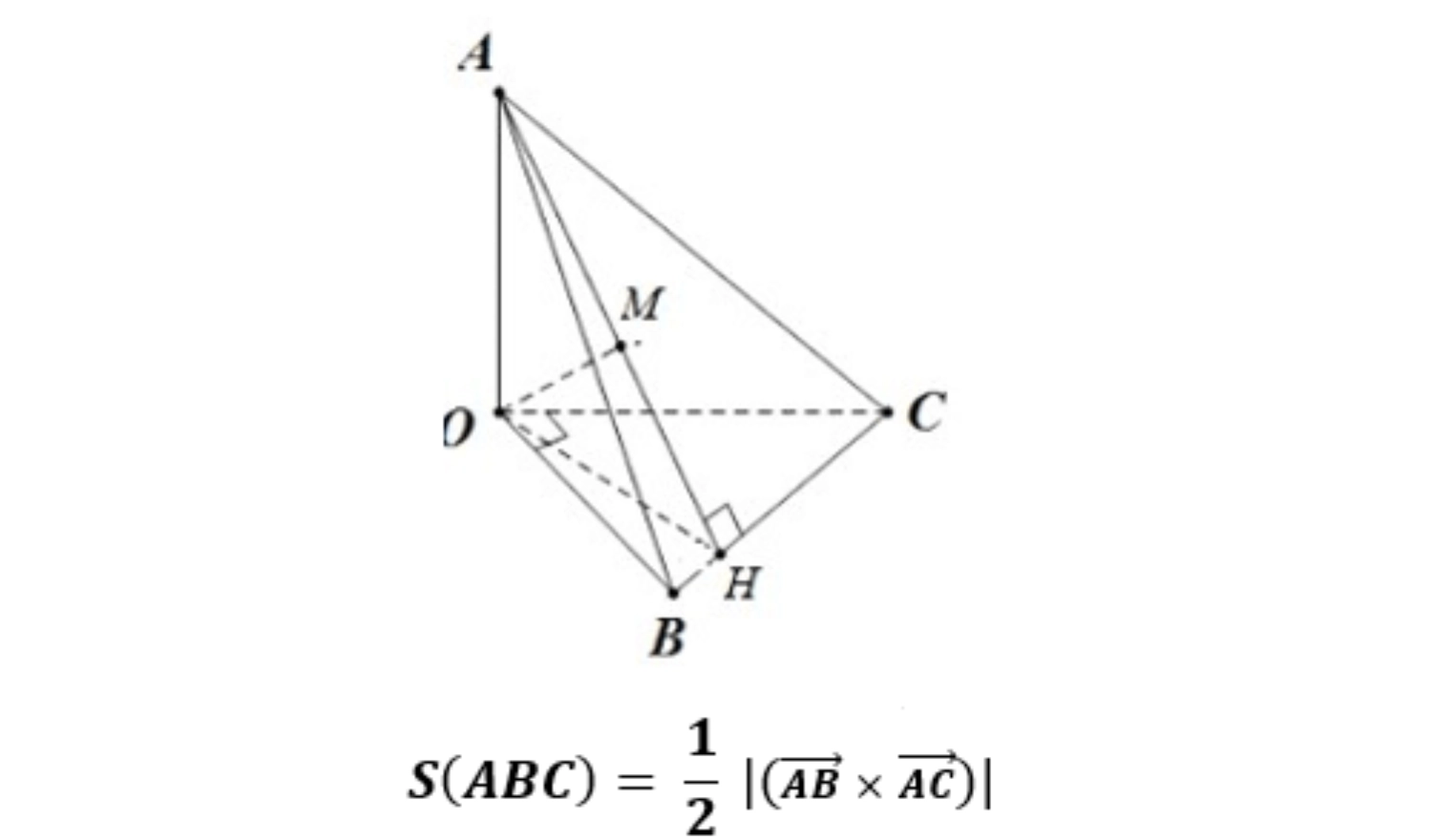
top-cong-thuc-tinh-dien-tich-tam-giac-moi-nhat-he-toa-do

Ví dụ: Trên hệ trục tọa độ cho tam giác ABC có 3 điểm A(-1; 1; 2), B(1; 2; 3), C(3; – 2; 0). Diện tích tam giác ABC được tính như sau:

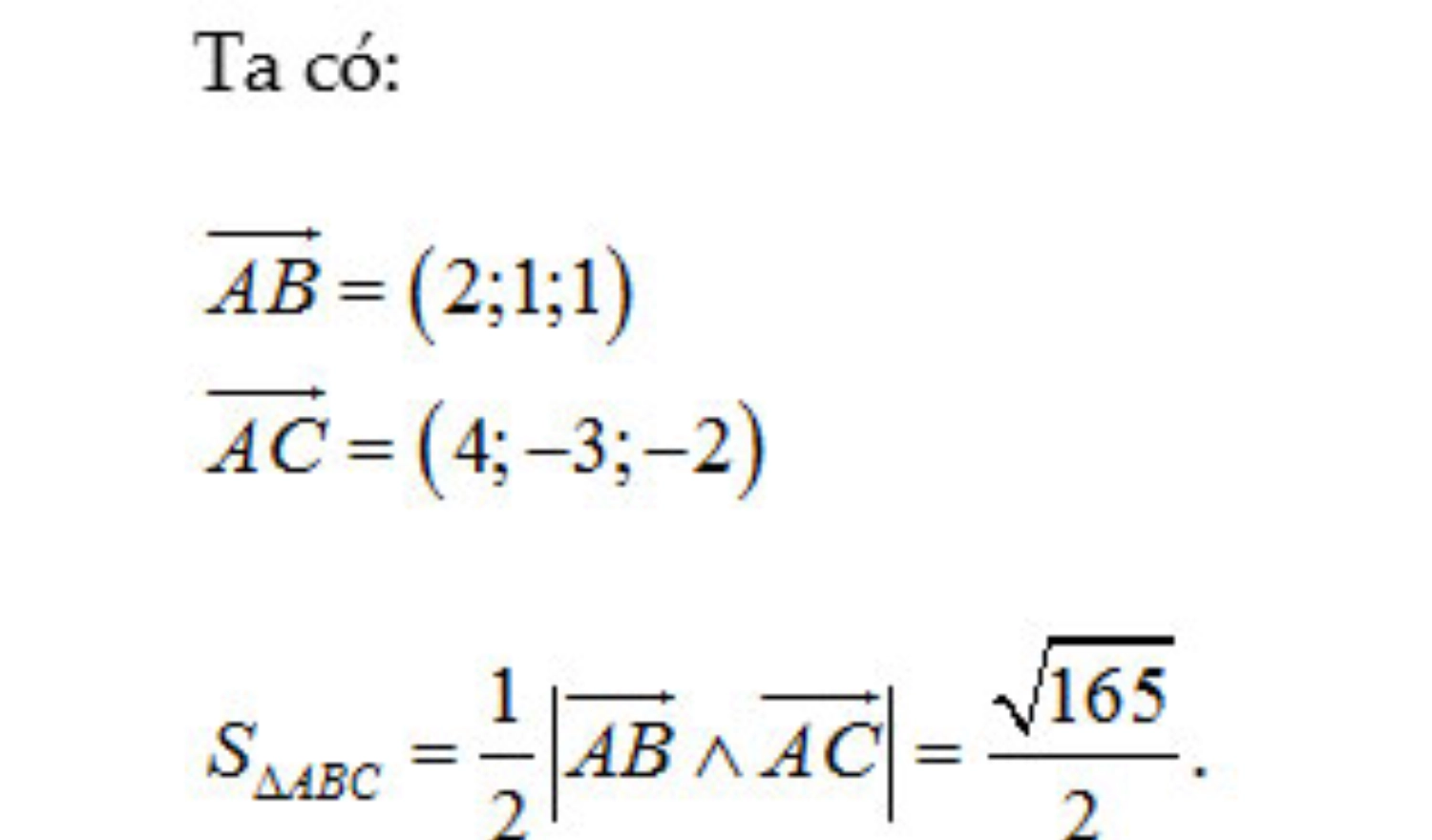
top-cong-thuc-tinh-dien-tich-tam-giac-moi-nhat-vi-du-he-toa-do

Công thức tính diện tích tam giác theo công thức HERON

Đối với tam giác ABC có ba cạnh a, b và c, và nửa chu vi là p (p = (a + b + c) / 2), diện tích tam giác được tính bằng công thức Heron: S= √(p x (p – a) x (p – b) x (p – c)).

Trong đó: p= (a+b+c)/2 là nửa chu vi của tam giác

Ví dụ: Tam giác ABC có độ dài ba cạnh là: AB = 6 cm, BC = 8 cm và AC = 10 cm. Tính diện tích của tam giác ABC.

Giải:

Nửa chu vi p của tam giác là: (6+8+10)/2= 12 cm

Diện tích tam giác ABC theo công thức HERON: S = √(12 x (12 – 6) x (12 – 8) x (12 – 10)) = 24cm²

Công thức tính diện tích tam giác theo cạnh và góc

Nếu bạn biết một góc và hai cạnh trong tam giác ABC, bạn có thể sử dụng định lý Sin để tính diện tích. Công thức tính diện tích tam giác theo cạnh và góc: S = 1/2 x a x b x sinC.

Trong đó:

S: diện tích tam giác
a: chiều dài một cạnh của tam giác
b: chiều dài một cạnh của tam giác
C: góc xen giữa hai cạnh a và b

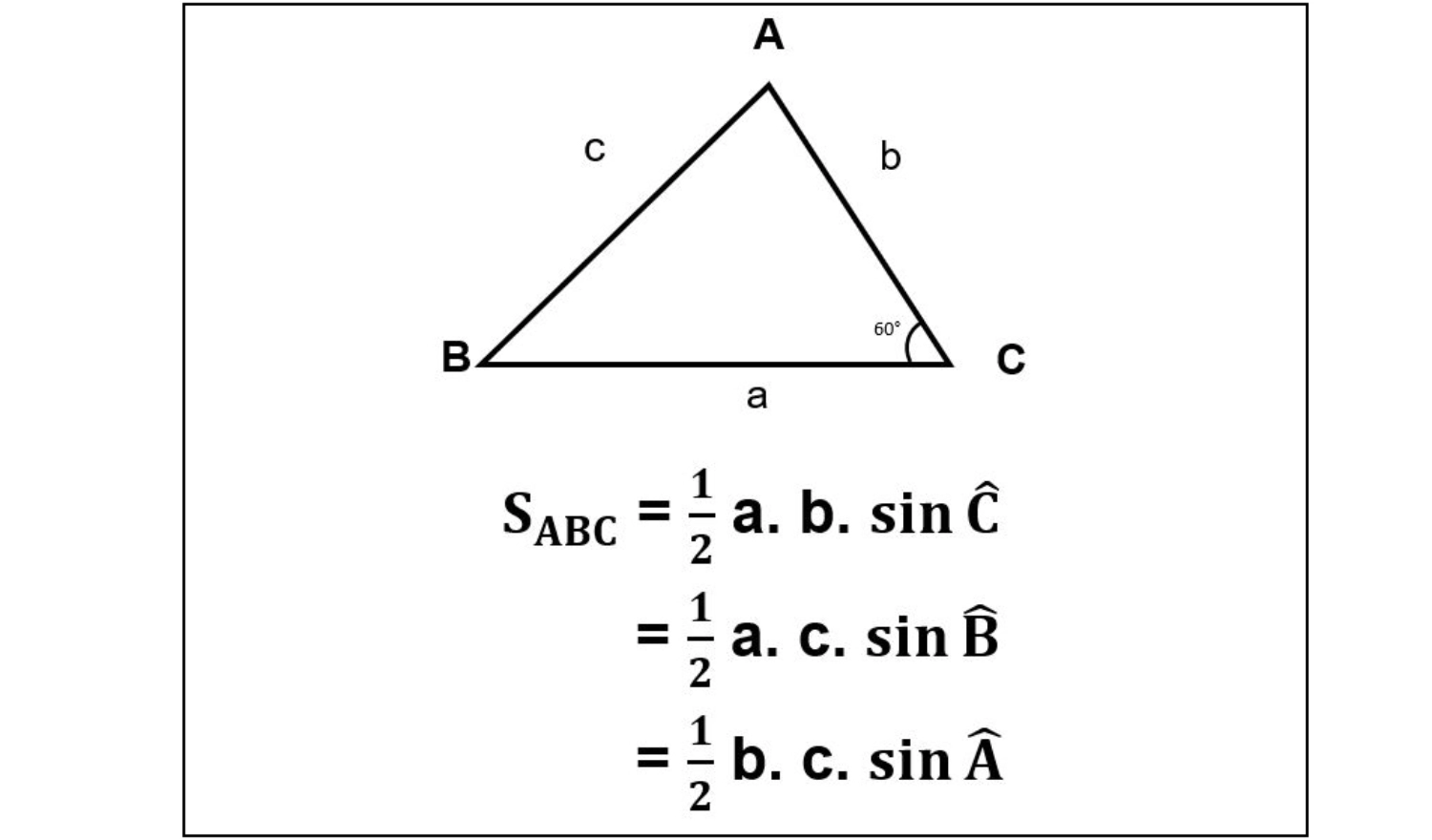
*Công thức tính diện tích theo cạnh và góc*

Ví dụ: Đối với tam giác có hai cạnh a = 6cm, b = 10cm, và góc xen giữa chúng là 60 độ, diện tích có thể được tính như sau: S = 1/2 x 6 x 10 x sin(60) = 25,9 cm²

Tổng kết

Trên đây là các cách công thức tính diện tích tam giác đơn giản nhất có ví dụ chi tiết mà chúng tôi đưa ra, có cả những công thức thu gọn để các bạn dễ áp dụng. Nếu thấy bài viết công thức tính diện tích tam giác hay, dễ hiểu, hãy theo dõi MobileCity để biết thêm nhiều thủ thuật nhé!

Xem thêm bài viết

Được viết bởi

Bùi Hà My

Giới thiệu ngắn về Bùi Hà My Bùi Hà My là nhân viên Content Marketing của MobileCity. Mình rất thích viết, mình muốn biến những suy nghĩ trong đầu thành những bài viết để từ đó giúp mọi người hiểu thêm về một vấn đề nào đó. Mình luôn cố gắng nỗ lực, lắng nghe góp ý của mọi người để từ đó hoàn thiện bản thân hơn. Mình luôn không ngừng thay đổi bản thân để thích nghi với cuộc sống hiện ...